Radius Of A Regular Polygon

Equiangular and equilateral polygon

Regular polygon

Edges and vertices	${\displaystyle n}$
Schläfli symbol	${\displaystyle \{due north\}}$
Coxeter–Dynkin diagram
Symmetry grouping	Dnorth, order 2n
Dual polygon	Cocky-dual
Surface area (with side length ${\displaystyle s}$ )	${\displaystyle A={\tfrac {one}{four}}ns^{ii}\cot \left({\frac {\pi }{northward}}\correct)}$
Internal angle	${\displaystyle (n-two)\times {\frac {\pi }{n}}}$
Internal bending sum	${\displaystyle \left(northward-ii\right)\times {\pi }}$
Inscribed circle bore	${\displaystyle d_{\text{IC}}=south\cot \left({\frac {\pi }{northward}}\right)}$
Circumscribed circle bore	${\displaystyle d_{\text{OC}}=south\csc \left({\frac {\pi }{north}}\right)}$
Backdrop	Convex, circadian, equilateral, isogonal, isotoxal

In Euclidean geometry, a regular polygon is a polygon that is direct equiangular (all angles are equal in measure out) and equilateral (all sides accept the same length). Regular polygons may exist either convex, star or skew. In the limit, a sequence of regular polygons with an increasing number of sides approximates a circumvolve, if the perimeter or area is stock-still, or a regular apeirogon (effectively a straight line), if the edge length is fixed.

General properties [edit]

Regular convex and star polygons with 3 to 12 vertices labelled with their Schläfli symbols

These properties utilize to all regular polygons, whether convex or star.

A regular n-sided polygon has rotational symmetry of social club n.

All vertices of a regular polygon lie on a common circle (the circumscribed circumvolve); i.e., they are concyclic points. That is, a regular polygon is a circadian polygon.

Together with the property of equal-length sides, this implies that every regular polygon as well has an inscribed circle or incircle that is tangent to every side at the midpoint. Thus a regular polygon is a tangential polygon.

A regular n-sided polygon can be synthetic with compass and straightedge if and merely if the odd prime number factors of n are distinct Fermat primes. See constructible polygon.

A regular n-sided polygon tin can be constructed with origami if and merely if ${\displaystyle north=2^{a}3^{b}p_{one}\cdots p_{r}}$ for some ${\displaystyle r\in \mathbb {N} }$ , where each distinct ${\displaystyle p_{i}}$ is a Pierpont prime number.^[ane]

Symmetry [edit]

The symmetry grouping of an n-sided regular polygon is dihedral group D _n (of order 2n): D₂, D₃, D₄, ... Information technology consists of the rotations in C _n , together with reflection symmetry in n axes that laissez passer through the centre. If north is even so half of these axes pass through two opposite vertices, and the other half through the midpoint of opposite sides. If n is odd and then all axes pass through a vertex and the midpoint of the reverse side.

Regular convex polygons [edit]

All regular uncomplicated polygons (a simple polygon is one that does not intersect itself anywhere) are convex. Those having the same number of sides are also like.

An n-sided convex regular polygon is denoted by its Schläfli symbol {north}. For north < 3, we accept 2 degenerate cases:

Monogon {1}

Degenerate in ordinary infinite. (Well-nigh authorities practise not regard the monogon as a true polygon, partly considering of this, and also considering the formulae below do non work, and its structure is not that of whatever abstruse polygon.)

Digon {2}; a "double line segment"

Degenerate in ordinary infinite. (Some regime do not regard the digon equally a true polygon because of this.)

In certain contexts all the polygons considered will be regular. In such circumstances it is customary to drib the prefix regular. For example, all the faces of compatible polyhedra must exist regular and the faces will exist described just as triangle, foursquare, pentagon, etc.

Every bit a corollary of the annulus chord formula, the area bounded past the circumcircle and incircle of every unit convex regular polygon is π/4

Angles [edit]

For a regular convex due north-gon, each interior bending has a measure of:

${\displaystyle {\frac {180(n-2)}{n}}}$ degrees;

${\displaystyle {\frac {(n-2)\pi }{n}}}$ radians; or

${\displaystyle {\frac {(n-ii)}{2n}}}$ full turns,

and each outside angle (i.east., supplementary to the interior bending) has a measure of ${\displaystyle {\tfrac {360}{n}}}$ degrees, with the sum of the exterior angles equal to 360 degrees or 2π radians or one full turn.

As north approaches infinity, the internal bending approaches 180 degrees. For a regular polygon with ten,000 sides (a myriagon) the internal angle is 179.964°. Every bit the number of sides increment, the internal angle tin can come very close to 180°, and the shape of the polygon approaches that of a circle. However the polygon can never become a circle. The value of the internal angle can never become exactly equal to 180°, as the circumference would effectively become a straight line. For this reason, a circle is not a polygon with an infinite number of sides.

Diagonals [edit]

For north > two, the number of diagonals is ${\displaystyle {\tfrac {i}{2}}n(n-3)}$ ; i.e., 0, ii, five, 9, ..., for a triangle, square, pentagon, hexagon, ... . The diagonals divide the polygon into 1, four, 11, 24, ... pieces OEIS: A007678.

For a regular due north-gon inscribed in a unit-radius circle, the product of the distances from a given vertex to all other vertices (including adjacent vertices and vertices connected by a diagonal) equals n.

Points in the plane [edit]

For a regular elementary northward-gon with circumradius R and distances d_i from an arbitrary point in the airplane to the vertices, we have^[two]

${\displaystyle {\frac {1}{n}}\sum _{i=i}^{due north}d_{i}^{four}+3R^{iv}=\left({\frac {1}{n}}\sum _{i=1}^{n}d_{i}^{2}+R^{two}\right)^{ii}.}$

For higher powers of distances ${\displaystyle d_{i}}$ from an arbitrary point in the plane to the vertices of a regular ${\displaystyle northward}$ -gon, if

${\displaystyle S_{n}^{(2m)}={\frac {i}{n}}\sum _{i=1}^{north}d_{i}^{2m}}$ ,

so^[3]

${\displaystyle S_{north}^{(2m)}=\left(S_{north}^{(two)}\right)^{g}+\sum _{k=1}^{\left\lfloor {\frac {m}{2}}\right\rfloor }{\binom {thou}{2k}}{\binom {2k}{k}}R^{2k}\left(S_{n}^{(two)}-R^{2}\right)^{k}\left(S_{n}^{(ii)}\right)^{m-2k}}$ ,

and

${\displaystyle S_{n}^{(2m)}=\left(S_{northward}^{(ii)}\right)^{1000}+\sum _{k=1}^{\left\lfloor {\frac {m}{2}}\right\rfloor }{\frac {one}{ii^{m}}}{\binom {m}{2k}}{\binom {2k}{1000}}\left(S_{n}^{(four)}-\left(S_{n}^{(two)}\correct)^{ii}\right)^{k}\left(S_{northward}^{(2)}\correct)^{grand-2k}}$ ,

where ${\displaystyle 1000}$ is a positive integer less than ${\displaystyle north}$ .

If ${\displaystyle L}$ is the distance from an arbitrary point in the plane to the centroid of a regular ${\displaystyle n}$ -gon with circumradius ${\displaystyle R}$ , then^[iii]

${\displaystyle \sum _{i=1}^{due north}d_{i}^{2m}=due north\left(\left(R^{two}+L^{2}\right)^{m}+\sum _{k=one}^{\left\lfloor {\frac {thou}{2}}\right\rfloor }{\binom {thou}{2k}}{\binom {2k}{k}}R^{2k}Fifty^{2k}\left(R^{2}+50^{two}\right)^{grand-2k}\right)}$ ,

where ${\displaystyle m}$ = 1, ii, …, ${\displaystyle n-ane}$ .

Interior points [edit]

For a regular n-gon, the sum of the perpendicular distances from any interior point to the due north sides is north times the apothem^{[4] : p. 72} (the apothem existence the distance from the centre to any side). This is a generalization of Viviani's theorem for the n = 3 case.^{[v] [6]}

Circumradius [edit]

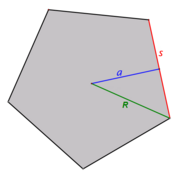
The circumradius R from the center of a regular polygon to one of the vertices is related to the side length due south or to the apothem a by

${\displaystyle R={\frac {due south}{2\sin \left({\frac {\pi }{north}}\correct)}}={\frac {a}{\cos \left({\frac {\pi }{n}}\right)}}\quad _{,}\quad a={\frac {s}{2\tan \left({\frac {\pi }{n}}\correct)}}}$

For constructible polygons, algebraic expressions for these relationships exist; see Bicentric polygon#Regular polygons.

The sum of the perpendiculars from a regular n-gon'south vertices to whatever line tangent to the circumcircle equals n times the circumradius.^{[4] : p. 73}

The sum of the squared distances from the vertices of a regular northward-gon to any point on its circumcircle equals 2nR ² where R is the circumradius.^{[4] : p.73}

The sum of the squared distances from the midpoints of the sides of a regular n-gon to any indicate on the circumcircle is 2nR ² − 1 / 4 ns ², where south is the side length and R is the circumradius.^{[4] : p. 73}

If ${\displaystyle d_{i}}$ are the distances from the vertices of a regular ${\displaystyle n}$ -gon to whatsoever point on its circumcircle, so ^[iii]

${\displaystyle 3\left(\sum _{i=one}^{n}d_{i}^{two}\right)^{2}=2n\sum _{i=i}^{northward}d_{i}^{4}}$ .

Dissections [edit]

Coxeter states that every zonogon (a 2m-gon whose reverse sides are parallel and of equal length) can be dissected into ${\displaystyle {\tbinom {north}{ii}}}$ or 1 / 2 m(m − 1) parallelograms. These tilings are contained as subsets of vertices, edges and faces in orthogonal projections thou-cubes.^[vii] In detail, this is true for any regular polygon with an even number of sides, in which case the parallelograms are all rhombi. The listing OEIS: A006245 gives the number of solutions for smaller polygons.

Example dissections for select even-sided regular polygons

21000	6	8	10	12	14	16	eighteen	20	24	30	twoscore	fifty
Image
Rhombs	3	6	10	xv	21	28	36	45	66	105	190	300

Expanse [edit]

The surface area A of a convex regular n-sided polygon having side s, circumradius R, apothem a, and perimeter p is given by^{[8] [9]}

${\displaystyle A={\tfrac {1}{2}}nsa={\tfrac {one}{2}}pa={\tfrac {ane}{iv}}ns^{2}\cot \left({\tfrac {\pi }{n}}\right)=na^{two}\tan \left({\tfrac {\pi }{n}}\correct)={\tfrac {1}{2}}nR^{two}\sin \left({\tfrac {two\pi }{north}}\right)}$

For regular polygons with side south = ane, circumradius R = ane, or apothem a = ane, this produces the post-obit table:^[10] (Note that since ${\displaystyle \cot ten\rightarrow 1/x}$ equally ${\displaystyle x\rightarrow 0}$ , the area when ${\displaystyle due south=i}$ tends to ${\displaystyle n^{2}/4\pi }$ as ${\displaystyle due north}$ grows large.)

Comparing of sizes of regular polygons with the aforementioned border length, from iii to threescore sides. The size increases without spring equally the number of sides approaches infinity.

Of all north-gons with a given perimeter, the one with the largest surface area is regular.^[19]

Constructible polygon [edit]

Some regular polygons are easy to construct with compass and straightedge; other regular polygons are not constructible at all. The ancient Greek mathematicians knew how to construct a regular polygon with iii, four, or 5 sides,^{[20] : p. 11} and they knew how to construct a regular polygon with double the number of sides of a given regular polygon.^{[xx] : pp. 49–fifty} This led to the question being posed: is it possible to construct all regular n-gons with compass and straightedge? If not, which n-gons are constructible and which are not?

Carl Friedrich Gauss proved the constructibility of the regular 17-gon in 1796. Five years afterwards, he developed the theory of Gaussian periods in his Disquisitiones Arithmeticae. This theory allowed him to formulate a sufficient condition for the constructibility of regular polygons:

A regular n-gon tin exist synthetic with compass and straightedge if due north is the product of a power of two and whatever number of distinct Fermat primes (including none).

(A Fermat prime is a prime of the form ${\displaystyle 2^{\left(2^{n}\correct)}+1.}$ ) Gauss stated without proof that this condition was too necessary, but never published his proof. A full proof of necessity was given by Pierre Wantzel in 1837. The effect is known as the Gauss–Wantzel theorem.

Equivalently, a regular n-gon is constructible if and only if the cosine of its mutual angle is a constructible number—that is, tin can be written in terms of the four bones arithmetic operations and the extraction of square roots.

Regular skew polygons [edit]

A regular skew polygon in 3-space can be seen every bit nonplanar paths zig-zagging betwixt two parallel planes, defined as the side-edges of a uniform antiprism. All edges and internal angles are equal.

The Ideal solids (the tetrahedron, cube, octahedron, dodecahedron, and icosahedron) have Petrie polygons, seen in cherry hither, with sides four, 6, 8, ten, and 10 respectively.

More mostly regular skew polygons tin can be divers in n-space. Examples include the Petrie polygons, polygonal paths of edges that divide a regular polytope into two halves, and seen as a regular polygon in orthogonal projection.

In the infinite limit regular skew polygons go skew apeirogons.

Regular star polygons [edit]

Regular star polygons

ii < 2q < p, gcd(p, q) = 1 {5/2} {vii/2} {vii/3}...
Schläfli symbol	{p/q}
Vertices and Edges	p
Density	q
Coxeter diagram
Symmetry group	Dihedral (Dp)
Dual polygon	Cocky-dual
Internal angle (degrees)	${\displaystyle 180-{\frac {360q}{p}}}$ [21]

A not-convex regular polygon is a regular star polygon. The well-nigh common instance is the pentagram, which has the same vertices as a pentagon, but connects alternate vertices.

For an n-sided star polygon, the Schläfli symbol is modified to indicate the density or "starriness" m of the polygon, as {due north/k}. If m is 2, for example, then every 2d betoken is joined. If m is iii, then every third point is joined. The purlieus of the polygon winds effectually the middle k times.

The (not-degenerate) regular stars of upwardly to 12 sides are:

• Pentagram – {5/2}
• Heptagram – {7/2} and {7/3}
• Octagram – {8/3}
• Enneagram – {9/2} and {ix/four}
• Decagram – {x/3}
• Hendecagram – {11/2}, {11/three}, {11/4} and {11/five}
• Dodecagram – {12/5}

g and n must be coprime, or the figure volition degenerate.

The degenerate regular stars of up to 12 sides are:

• Tetragon – {four/two}
• Hexagons – {6/two}, {half dozen/3}
• Octagons – {viii/2}, {8/iv}
• Enneagon – {9/three}
• Decagons – {10/2}, {10/4}, and {10/5}
• Dodecagons – {12/2}, {12/3}, {12/4}, and {12/half-dozen}

Two interpretations of {6/2}

Grünbaum {six/2} or 2{iii}[22]	Coxeter 2{iii} or {half dozen}[2{3}]{6}
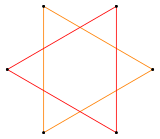Doubly-wound hexagon	Hexagram as a compound of two triangles

Depending on the precise derivation of the Schläfli symbol, opinions differ every bit to the nature of the degenerate figure. For example, {half-dozen/two} may be treated in either of two means:

• For much of the 20th century (see for instance Coxeter (1948)), nosotros have unremarkably taken the /ii to indicate joining each vertex of a convex {vi} to its most neighbors two steps away, to obtain the regular compound of ii triangles, or hexagram. Coxeter clarifies this regular compound with a notation {kp}[thousand{p}]{kp} for the chemical compound {p/thou}, so the hexagram is represented every bit {vi}[2{3}]{half dozen}.^[23] More compactly Coxeter also writes 2{northward/2}, like 2{3} for a hexagram as compound equally alternations of regular even-sided polygons, with italics on the leading factor to differentiate it from the coinciding estimation.^[24]
• Many modern geometers, such equally Grünbaum (2003),^[22] regard this as incorrect. They have the /2 to indicate moving two places around the {half dozen} at each step, obtaining a "double-wound" triangle that has 2 vertices superimposed at each corner point and ii edges along each line segment. Not simply does this fit in amend with modernistic theories of abstract polytopes, only information technology besides more closely copies the way in which Poinsot (1809) created his star polygons – past taking a unmarried length of wire and bending it at successive points through the aforementioned angle until the figure closed.

Duality of regular polygons [edit]

All regular polygons are self-dual to congruency, and for odd north they are self-dual to identity.

In addition, the regular star figures (compounds), being composed of regular polygons, are also self-dual.

Regular polygons as faces of polyhedra [edit]

A uniform polyhedron has regular polygons every bit faces, such that for every two vertices there is an isometry mapping one into the other (merely every bit at that place is for a regular polygon).

A quasiregular polyhedron is a uniform polyhedron which has just two kinds of face alternating effectually each vertex.

A regular polyhedron is a uniform polyhedron which has simply one kind of face.

The remaining (not-compatible) convex polyhedra with regular faces are known equally the Johnson solids.

A polyhedron having regular triangles every bit faces is called a deltahedron.

Meet as well [edit]

• Euclidean tilings by convex regular polygons
• Platonic solid
• Apeirogon – An space-sided polygon can besides be regular, {∞}.
• Listing of regular polytopes and compounds
• Equilateral polygon
• Carlyle circle

Notes [edit]

1. ^ Hwa, Young Lee (2017). Origami-Constructible Numbers (PDF) (MA thesis). University of Georgia. pp. 55–59.
2. ^ Park, Poo-Sung. "Regular polytope distances", Forum Geometricorum 16, 2016, 227-232. http://forumgeom.fau.edu/FG2016volume16/FG201627.pdf
3. ^ ^{a b c} Meskhishvili, Mamuka (2020). "Cyclic Averages of Regular Polygons and Platonic Solids". Communications in Mathematics and Applications. 11: 335–355.
4. ^ ^{a b c d} Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ., 2007 (orig. 1929).
5. ^ Pickover, Clifford A, The Math Book, Sterling, 2009: p. 150
6. ^ Chen, Zhibo, and Liang, Tian. "The antipodal of Viviani'southward theorem", The College Mathematics Periodical 37(5), 2006, pp. 390–391.
7. ^ Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141
8. ^ "Math Open Reference". Retrieved 4 Feb 2014.
9. ^ "Mathwords".
10. ^ Results for R = 1 and a = ane obtained with Maple, using function definition:

                                            f                    :=                    proc                    (                    n                    )                    options                    operator                    ,                    arrow                    ;                    [                    [                    convert                    (                    i                    /                    4                    *                    northward                    *                    cot                    (                    Pi                    /                    n                    )                    ,                    radical                    )                    ,                    convert                    (                    1                    /                    4                    *                    north                    *                    cot                    (                    Pi                    /                    n                    )                    ,                    float                    )]                    ,                    [                    convert                    (                    1                    /                    ii                    *                    n                    *                    sin                    (                    2                    *                    Pi                    /                    n                    )                    ,                    radical                    )                    ,                    catechumen                    (                    i                    /                    2                    *                    n                    *                    sin                    (                    ii                    *                    Pi                    /                    n                    )                    ,                    float                    )                    ,                    catechumen                    (                    one                    /                    ii                    *                    north                    *                    sin                    (                    2                    *                    Pi                    /                    north                    )                    /                    Pi                    ,                    float                    )]                    ,                    [                    convert                    (                    n                    *                    tan                    (                    Pi                    /                    n                    )                    ,                    radical                    )                    ,                    convert                    (                    northward                    *                    tan                    (                    Pi                    /                    n                    )                    ,                    float                    )                    ,                    convert                    (                    n                    *                    tan                    (                    Pi                    /                    north                    )                    /                    Pi                    ,                    float                    )]                    ]                    cease                    proc                  

    The expressions for n = xvi are obtained past twice applying the tangent half-angle formula to tan(π/four)
11. ^ ${\displaystyle {\tfrac {15}{8}}\left({\sqrt {15}}+{\sqrt {three}}+{\sqrt {two\left(5+{\sqrt {5}}\right)}}\right)}$
12. ^ ${\displaystyle {\tfrac {15}{16}}\left({\sqrt {15}}+{\sqrt {3}}-{\sqrt {10-2{\sqrt {5}}}}\right)}$
13. ^ ${\displaystyle {\tfrac {15}{two}}\left(3{\sqrt {3}}-{\sqrt {15}}-{\sqrt {2\left(25-eleven{\sqrt {v}}\correct)}}\right)}$
14. ^ ${\displaystyle 4\left(i+{\sqrt {2}}+{\sqrt {2\left(2+{\sqrt {2}}\correct)}}\right)}$
15. ^ ${\displaystyle 16\left(i+{\sqrt {two}}\right)\left({\sqrt {2\left(2-{\sqrt {2}}\right)}}-one\correct)}$
16. ^ ${\displaystyle five\left(1+{\sqrt {5}}+{\sqrt {5+2{\sqrt {v}}}}\right)}$
17. ^ ${\displaystyle {\tfrac {v}{two}}\left({\sqrt {v}}-1\right)}$
18. ^ ${\displaystyle xx\left(1+{\sqrt {5}}-{\sqrt {5+ii{\sqrt {v}}}}\right)}$
19. ^ Chakerian, G.D. "A Distorted View of Geometry." Ch. 7 in Mathematical Plums (R. Honsberger, editor). Washington, DC: Mathematical Association of America, 1979: 147.
20. ^ ^{a b} Bold, Benjamin. Famous Problems of Geometry and How to Solve Them, Dover Publications, 1982 (orig. 1969).
21. ^ Kappraff, Jay (2002). Beyond measure: a guided tour through nature, myth, and number. World Scientific. p. 258. ISBN978-981-02-4702-7.
22. ^ ^{a b} Are Your Polyhedra the Same as My Polyhedra? Branko Grünbaum (2003), Fig. 3
23. ^ Regular polytopes, p.95
24. ^ Coxeter, The Densities of the Regular Polytopes 2, 1932, p.53

References [edit]

• Lee, Hwa Young; "Origami-Constructible Numbers".
• Coxeter, H.S.Thousand. (1948). "Regular Polytopes". Methuen and Co.
• Grünbaum, B.; Are your polyhedra the same as my polyhedra?, Discrete and comput. geom: the Goodman-Pollack festschrift, Ed. Aronov et al., Springer (2003), pp. 461–488.
• Poinsot, Fifty.; Memoire sur les polygones et polyèdres. J. de fifty'École Polytechnique 9 (1810), pp. 16–48.

External links [edit]

• Weisstein, Eric W. "Regular polygon". MathWorld.
• Regular Polygon clarification With interactive blitheness
• Incircle of a Regular Polygon With interactive blitheness
• Area of a Regular Polygon Three dissimilar formulae, with interactive animation
• Renaissance artists' constructions of regular polygons at Convergence

v t e Fundamental convex regular and compatible polytopes in dimensions 2–10
Family	A n	B n	I 2(p) / D n	E 6 / E 7 / E viii / F four / M 2	Hnorth
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform polychoron	Pentachoron	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Compatible 5-polytope	5-simplex	5-orthoplex • five-cube	v-demicube
Uniform vi-polytope	6-simplex	vi-orthoplex • six-cube	half-dozen-demicube	122 • 221
Uniform 7-polytope	7-simplex	7-orthoplex • vii-cube	vii-demicube	i32 • 231 • 321
Compatible 8-polytope	8-simplex	8-orthoplex • 8-cube	eight-demicube	ane42 • two41 • 421
Uniform 9-polytope	ix-simplex	9-orthoplex • 9-cube	9-demicube
Uniform ten-polytope	10-simplex	10-orthoplex • 10-cube	x-demicube
Uniform n-polytope	northward-simplex	north-orthoplex • due north-cube	n-demicube	ik2 • iik1 • k21	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds

Radius Of A Regular Polygon,

Source: https://en.wikipedia.org/wiki/Regular_polygon

Posted by: edwardsnots1968.blogspot.com

Share this post