How To Find Terminal Point Determined By T
Last POINTS ON THE UNIT Circumvolve
Suppose t is a real number. Let's mark off a distance t forth the unit circle, starting at the point (1, 0) and moving in a counterclockwise direction, if t is positive or in a clockwise direction, if t is negative.
In this style we make it at a betoken P(x, y) on the unit circle. The indicate P(x, y) obtained in this way is chosen the terminal betoken adamant by the real number t.
Terminal Point P(x, y) Determined by t > 0 :
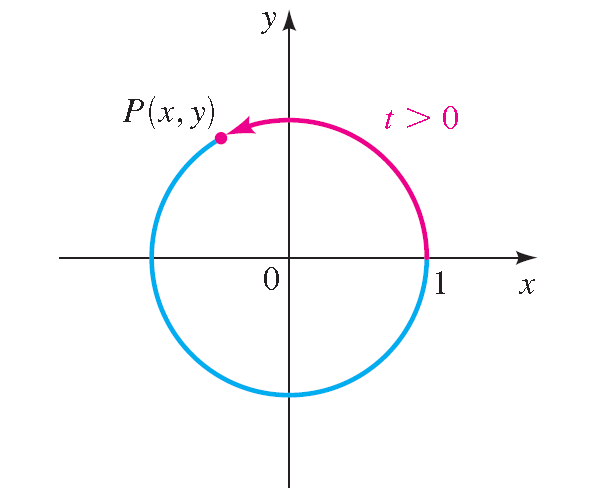
Last Signal P(ten, y) Determined by t < 0 :
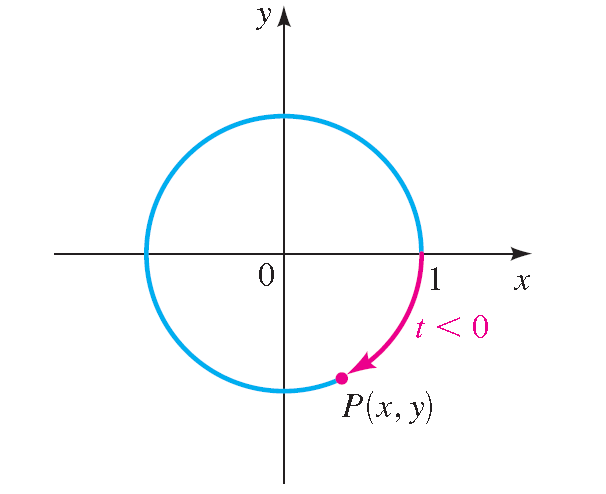
The circumference of the unit circle is
C = iiπ(1) = 2 π
So, if a point starts at (1, 0) and moves counter clockwise all the way around the unit circle and returns to (ane, 0), information technology travels a distance of iiπ. To motion halfway around the circle, it travels a altitude of (1/two)(2π) = π.
To move a quarter of the distance effectually the circle, information technology travels a distance of (1/iv)(iiπ) = π/2. Whither does the point end up when it travels these distances along the circle? In the diagram shown beneath, we see, for case, that when information technology travels a distance ofπ starting at (1, 0), its final point is (-1, 0).
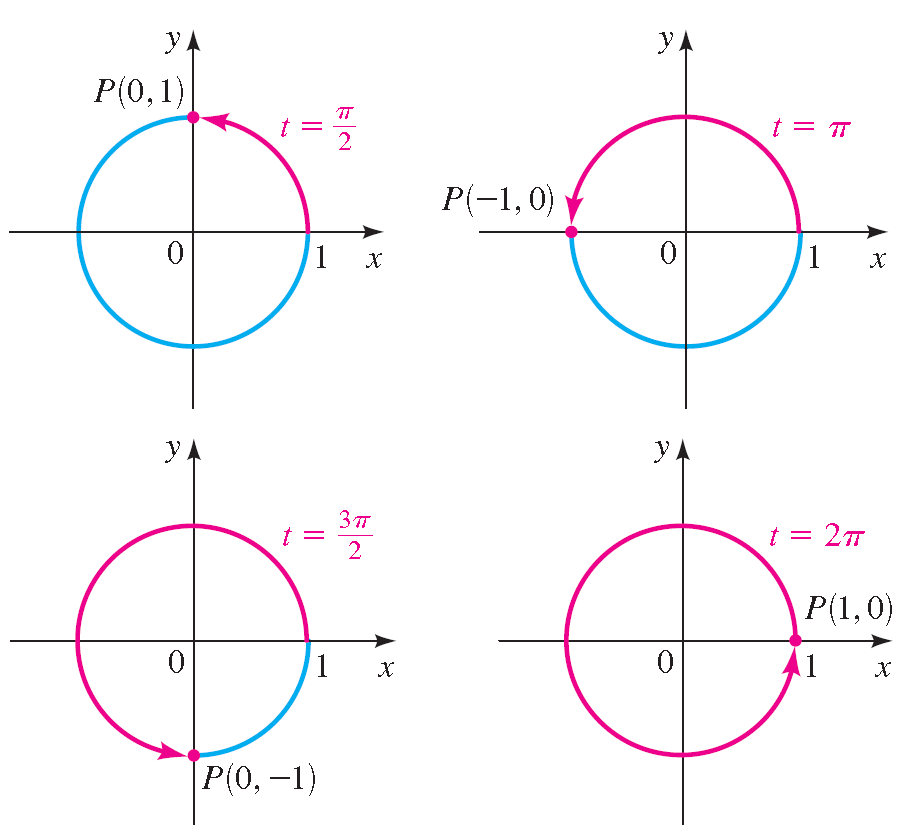
Finding Final Points
Find the terminal point on the unit circle determined by each real number t.
Case 1 :
t = 3π
Solution :
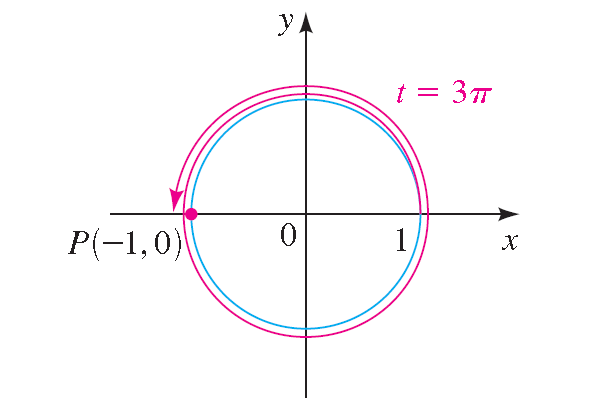
The terminal point determined by 3π is (-ane, -0).
Case 2 :
t = -π
Solution :
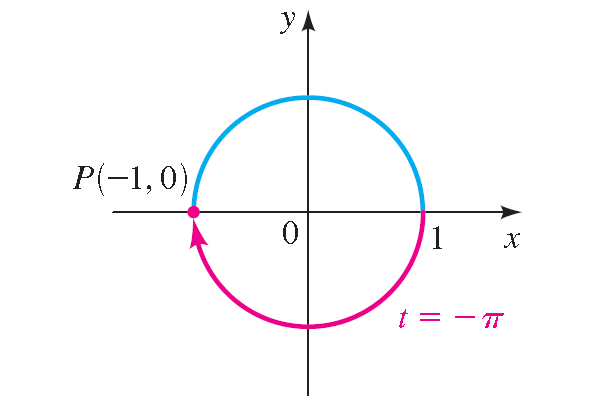
The concluding point determined by -π is (-1, -0).
Case 3 :
t = -π/2
Solution :
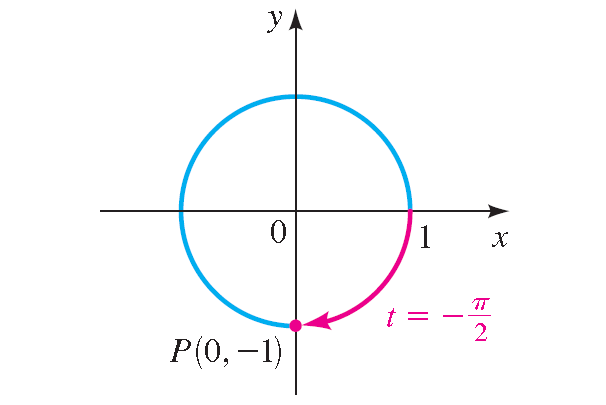
The terminal point determined by -π/two is (0, -1).
Notice that different values of t can determine the same terminal point.
The terminal bespeak P(10, y) adamant past t =π/four is the same distance from (1, 0) as from (0, 1) along the unit circle.
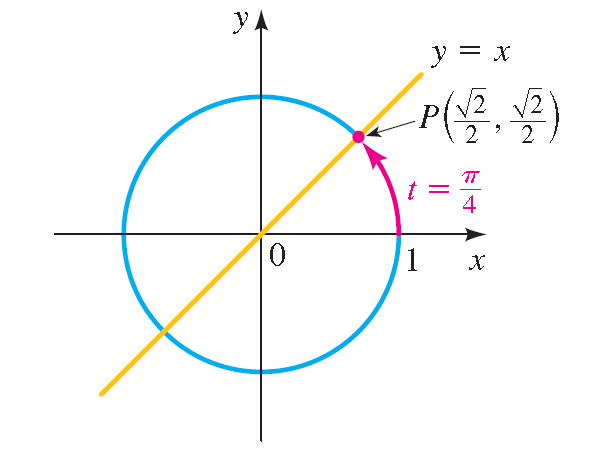
Since the unit circle is symmetric with respect to the line y = x, it follows that P lies on the line y = x. And so P is the point of intersection (in the first quadrant) of the circlex ii + y 2 = 1 and the line y = x.
Substituting x for y in the equation of the unit circle.
x 2 + x 2 = ane
2x2 = 1
xii = 1/2
k = ± 1/√2
Considering P is in the first quadrant, 10 = 1/√2 and y = x, we have y = ane/ √ 2 too.
Thus the terminal betoken determined by π/four is
P(1/ √ 2, 1/ √ ii) = P( √ ii/2, √ ii/2)
Similar methods can be used to observe the last points adamant past t = π/vi and t = π/3.
Tabular array :
| t 0 π/half dozen π/4 π/3 π/2 | Final point determined by t (1, 0) (√3/ii, i/two) (√ii/ii, √2/2) (1/2, √3/2) (0, 1) |
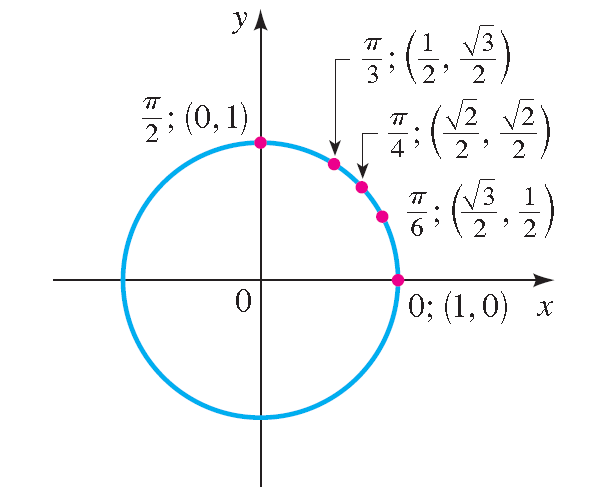
Example 4 :
t = -π/4
Solution :
Let P be the final point determined by - π/4, and let Q be the terminal indicate determined past π/iv. In the diagram shown below, we see that the point P has the same coordinates equally Q except for sign.
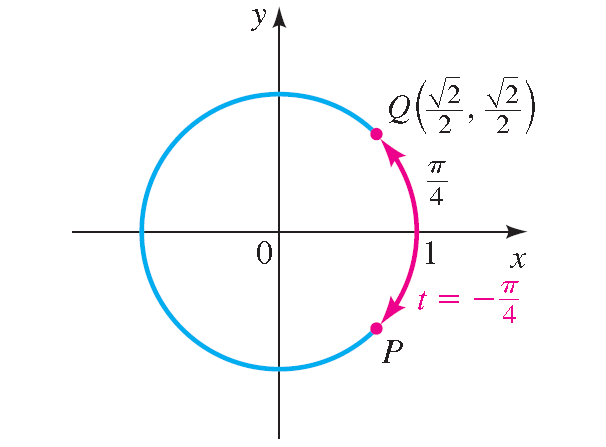
Because P is in quadrant IV, its x-coordinate is positive and its y-coordinate is negative. Thus, the terminal bespeak is
P( √2/ii, - √2/2)
Example 5 :
t = 3π/iv
Solution :
Let P be the final point determined by 3 π/iv, and allow Q be the terminal point determined by π/four. In the diagram shown below, we come across that the bespeak P has the aforementioned coordinates as Q except for sign.
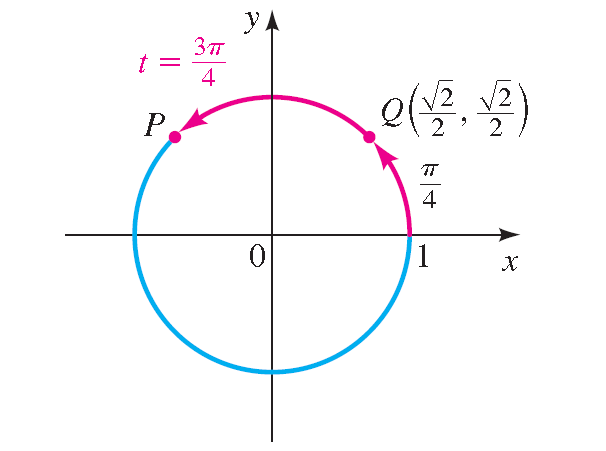
ConsideringP is in quadrant II, its x-coordinate is negative and its y-coordinate is positive. Thus, the terminal point is
P(-√2/2, √ii/ii)
Example half-dozen :
t = -5π/6
Solution :
Permit P be the terminal point determined by -five π/6, and let Q be the concluding point determined by π/vi. In the diagram shown below, we meet that the signal P has the same coordinates as Q except for sign.
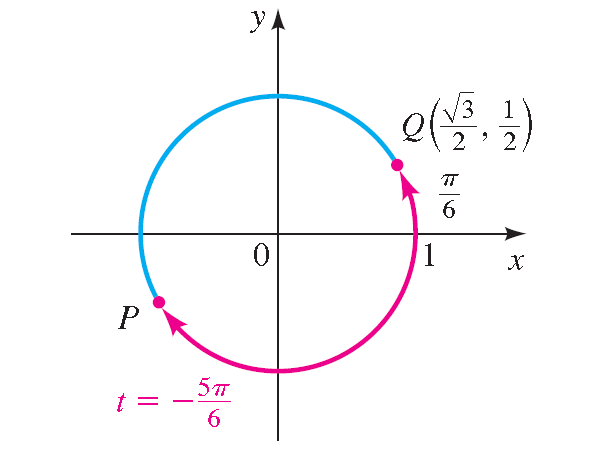
Because P is in quadrant Iii, its both x-coordinate and y-coordinate are negative. Thus, the terminal point is
P(- √iii/2, -i /2)
Kindly mail your feedback tov4formath@gmail.com
We ever appreciate your feedback.
© All rights reserved. onlinemath4all.com
Source: https://www.onlinemath4all.com/terminal-points-on-the-unit-circle.html

0 Response to "How To Find Terminal Point Determined By T"
Post a Comment