Standard Form Of A Hyperbola
Hyperbola
In mathematics, a hyperbola is an important conic section formed by the intersection of the double cone by a aeroplane surface, but not necessarily at the eye. A hyperbola is symmetric along the conjugate axis, and shares many similarities with the ellipse. Concepts like foci, directrix, latus rectum, eccentricity, apply to a hyperbola. A few common examples of hyperbola include the path followed by the tip of the shadow of a sundial, the scattering trajectory of sub-atomic particles, etc.
Hither we shall aim at understanding the definition, formula of a hyperbola, derivation of the formula, and standard forms of hyperbola using the solved examples.
| 1. | What is Hyperbola? |
| two. | Parts of Hyperbola |
| iii. | Standard Grade of Hyperbola Equation |
| 4. | Derivation of Hyperbola Equation |
| five. | Hyperbola Formula |
| half dozen. | Hyperbola Graph |
| 7. | Properties of a Hyperbola |
| 8. | FAQs on Hyperbola |
What is Hyperbola?
A hyperbola, a blazon of smooth curve lying in a plane, has two pieces, called connected components or branches, that are mirror images of each other and resemble 2 space bows. A hyperbola is a gear up of points whose difference of distances from two foci is a constant value. This difference is taken from the altitude from the further focus so the distance from the nearer focus. For a point P(10, y) on the hyperbola and for 2 foci F, F', the locus of the hyperbola is PF - PF' = 2a.
Hyperbola Definition
A hyperbola, in analytic geometry, is a conic department that is formed when a airplane intersects a double right round cone at an angle such that both halves of the cone are intersected. This intersection of the aeroplane and cone produces two split up unbounded curves that are mirror images of each other chosen a hyperbola.
Parts of a Hyperbola
Let us check through a few of import terms relating to the different parameters of a hyperbola.
Foci of hyperbola: The hyperbola has ii foci and their coordinates are F(c, o), and F'(-c, 0).
Heart of Hyperbola: The midpoint of the line joining the ii foci is called the center of the hyperbola.
Major Axis: The length of the major axis of the hyperbola is 2a units.
Minor Axis: The length of the minor axis of the hyperbola is 2b units.
Vertices: The points where the hyperbola intersects the axis are called the vertices. The vertices of the hyperbola are (a, 0), (-a, 0).
Latus Rectum of Hyperbola: The latus rectum is a line drawn perpendicular to the transverse axis of the hyperbola and is passing through the foci of the hyperbola. The length of the latus rectum of the hyperbola is 2bii/a.
Transverse Axis: The line passing through the 2 foci and the center of the hyperbola is called the transverse centrality of the hyperbola.
Conjugate Centrality: The line passing through the center of the hyperbola and perpendicular to the transverse centrality is called the cohabit axis of the hyperbola.
Eccentricity of Hyperbola: (due east > 1) The eccentricity is the ratio of the distance of the focus from the center of the hyperbola, and the altitude of the vertex from the center of the hyperbola. The altitude of the focus is 'c' units, and the distance of the vertex is 'a' units, and hence the eccentricity is e = c/a.
Hyperbola Equation
The below equation represents the general equation of a hyperbola. Hither the x-axis is the transverse axis of the hyperbola, and the y-centrality is the conjugate centrality of the hyperbola.
\(\dfrac{ten^2}{a^two} - \dfrac{y^2}{b^two} = 1\)
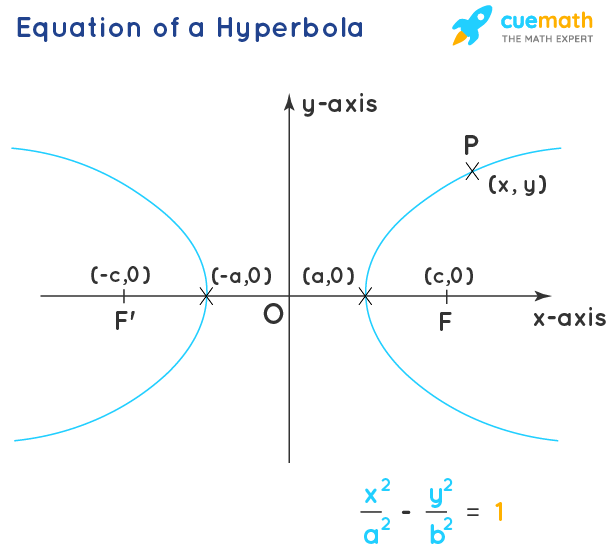
Permit u.s.a. empathise the standard form of the hyperbola equation and its derivation in detail in the following sections.
Standard Equation of Hyperbola
At that place are two standard equations of the Hyperbola. These equations are based on the transverse centrality and the conjugate axis of each of the hyperbola. The standard equation of the hyperbola is \(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\) has the transverse axis as the ten-axis and the conjugate axis is the y-axis. Further, another standard equation of the hyperbola is \(\dfrac{y^2}{a^2} - \dfrac{x^2}{b^2} = 1\) and it has the transverse axis equally the y-axis and its conjugate axis is the ten-centrality. The beneath prototype shows the two standard forms of equations of the hyperbola.

Derivation of Hyperbola Equation
Every bit per the definition of the hyperbola, permit us consider a point P on the hyperbola, and the difference of its distance from the ii foci F, F' is 2a.
PF' - PF = 2a
Let the coordinates of P be (x, y) and the foci be F(c, o) and F'(-c, 0)
\(\sqrt{(ten + c)^2 + y^2}\) - \(\sqrt{(x - c)^2 + y^ii}\) = 2a
\(\sqrt{(x + c)^ii + y^two}\) = 2a + \(\sqrt{(x - c)^two + y^ii}\)
Now nosotros need to foursquare on both sides to solve further.
(10 + c)ii + ytwo = 4a2 + (10 - c)2 + yii + 4a\(\sqrt{(10 - c)^2 + y^2}\)
x2 + c2 + 2cx + y2 = 4a2 + x2 + c2 - 2cx + y2 + 4a\(\sqrt{(x - c)^ii + y^2}\)
4cx - 4a2 = 4a\(\sqrt{(ten - c)^two + y^2}\)
cx - a2 = a\(\sqrt{(ten - c)^2 + y^2}\)
Squaring on both sides and simplifying, we have.
\(\dfrac{ten^two}{a^ii} - \dfrac{y^2}{c^2 - a^2} =1\)
Too, nosotros accept cii = aii + btwo, we tin can substitute this in the to a higher place equation.
\(\dfrac{x^two}{a^2} - \dfrac{y^2}{b^2} =1\)
Therefore, the standard equation of the Hyperbola is derived.
Hyperbola Formula
Hyperbola is an open up curve that has 2 branches that look similar mirror images of each other. For any point on any of the branches, the absolute departure between the point from foci is constant and equals to 2a, where a is the distance of the branch from the center. The Hyperbola formula helps us to discover diverse parameters and related parts of the hyperbola such as the equation of hyperbola, the major and minor centrality, eccentricity, asymptotes, vertex, foci, and semi-latus rectum.
Equation of hyperbola formula: (ten - \(x_0\))2 / atwo - ( y - \(y_0\))2 / b2 = 1
Major and minor centrality formula: y = y\(_0\) is the major centrality, and its length is 2a, whereas 10 = x\(_0\) is the minor axis, and its length is 2b
Eccentricity(eastward) of hyperbola formula: e = \(\sqrt {i + \dfrac {b^2}{a^2}}\)
Asymptotes of hyperbola formula:
y = y\(_0\) − (b / a)ten + (b / a)ten\(_0\)
y = y\(_0\) + (b / a)x - (b / a)x\(_0\)
Vertex of hyperbola formula:
(a, y\(_0\)) and (−a, y\(_0\))
Focus(foci) of hyperbola:
(x\(_0\) + \(\sqrt{a^2+b^two} \),y\(_0\)), and (x\(_0\) - \(\sqrt{a^two+b^2} \),y\(_0\))
Semi-latus rectum(p) of hyperbola formula:
p = b2 / a
where,
- 10\(_0\), y\(_0\) are the center points.
- a = semi-major axis.
- b = semi-minor centrality.
Case: The equation of the hyperbola is given as (x - 5)ii/4two - (y - 2)2/ iiii = 1. Employ the hyperbola formulas to find the length of the Major Centrality and Pocket-sized Centrality.
Solution:
Using the hyperbola formula for the length of the major and minor axis
Length of major axis = 2a, and length of minor centrality = 2b
Length of major axis = ii × 4 = 8, and Length of minor centrality = 2 × 2 = four
Reply: The length of the major axis is 8 units, and the length of the minor axis is 4 units.
Graph of Hyperbola
All hyperbolas share common features, consisting of 2 curves, each with a vertex and a focus. The transverse axis of a hyperbola is the centrality that crosses through both vertices and foci, and the conjugate axis of the hyperbola is perpendicular to information technology. Nosotros can notice the graphs of standard forms of hyperbola equation in the figure beneath. If the equation of the given hyperbola is not in standard form, and then we need to complete the square to get it into standard form.
Nosotros can observe the different parts of a hyperbola in the hyperbola graphs for standard equations given beneath.
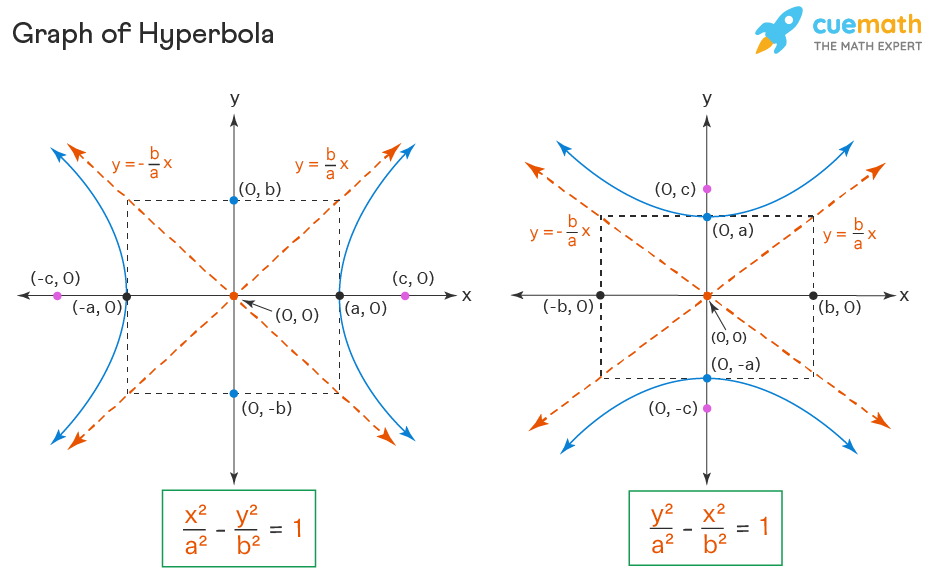
Here,
- If the foci lie on the ten-axis, the standard form of a hyperbola can exist given as,
\(\dfrac{(x-h)^2}{a^two} - \dfrac{(y-k)^2}{b^two} = ane\) - If the foci prevarication on the y-axis, the standard form of the hyperbola is given as,
\(\dfrac{(y-m)^2}{a^2} - \dfrac{(x-h)^2}{b^2} = ane\) - Coordinates of the center: (h, k).
- Coordinates of vertices: (h+a, yard) and (h - a,k)
- Co-vertices correspond to b, the " minor semi-axis length", and coordinates of co-vertices: (h,thou+b) and (h,k-b).
- Foci have coordinates (h+c,k) and (h-c,k). The value of c is given as, cii = a2 + bii.
- Slopes of asymptotes: y = ±(b/a)ten.
Properties of a Hyperbola
The following important backdrop related to different concepts help in understanding hyperbola better.
Asymptotes: The pair of straight lines drawn parallel to the hyperbola and assumed to bear upon the hyperbola at infinity. The equations of the asymptotes of the hyperbola are y = bx/a, and y = -bx/a respectively. 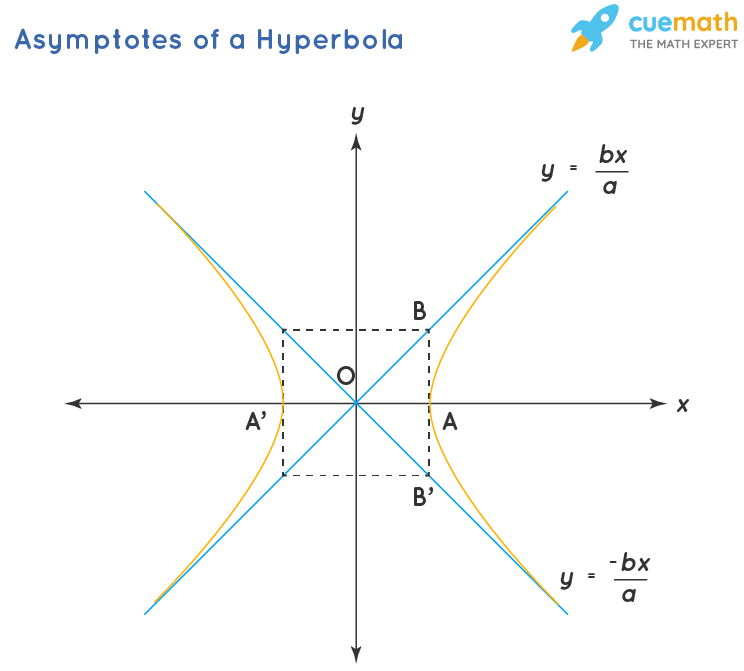
Rectangular Hyperbola: The hyperbola having the transverse centrality and the conjugate axis of the aforementioned length is chosen the rectangular hyperbola. Here, we have 2a = 2b, or a = b. Hence the equation of the rectangular hyperbola is equal to x2 - y2 = atwo
Parametric Coordinates: The points on the hyperbola can be represented with the parametric coordinates (x, y) = (asecθ, btanθ). These parametric coordinates representing the points on the hyperbola satisfy the equation of the hyperbola.
Auxilary Circumvolve: A circle drawn with the endpoints of the transverse axis of the hyperbola as its bore is chosen the auxiliary circle. The equation of the auxiliary circle of the hyperbola is tentwo + yii = a2.
Direction Circle: The locus of the indicate of intersection of perpendicular tangents to the hyperbola is called the manager circumvolve. The equation of the director circle of the hyperbola is xtwo + y2 = atwo - b2.
Related Articles on Hyperbola:
The following topics are helpful for a improve understanding of the hyperbola and its related concepts.
- Coordinate Geometry
- Conics in Existent Life
- Cartesian Coordinates
- Parabola
Examples on Hyperbola
get to slidego to slidego to slide

Breakdown tough concepts through simple visuals.
Math will no longer be a tough bailiwick, especially when y'all empathize the concepts through visualizations.
Book a Free Trial Class
Practice Questions on Hyperbola
go to slidego to slide
FAQs on Hyperbola
What is Hyperbola in Conic Section?
A hyperbola is the locus of a point whose deviation of the distances from two fixed points is a abiding value. The ii fixed points are called the foci of the hyperbola, and the equation of the hyperbola is \(\dfrac{x^2}{a^ii} - \dfrac{y^2}{b^2} = ane\). Here a is called the semi-major axis and b is called the semi-pocket-sized axis of the hyperbola.
What is the Equation of Hyperbola?
The equation of the hyperbola is \(\dfrac{x^2}{a^two} - \dfrac{y^ii}{b^ii} = 1\). Here 'a' is the sem-major axis, and 'b' is the semi-minor centrality. There are ii standard forms of equations of a hyperbola.
How to Find the General Equation of a Hyperbola?
The equation of the hyperbola can exist derived from the basic definition of a hyperbola: A hyperbola is the locus of a point whose divergence of the distances from 2 stock-still points is a constant value. Let the fixed point be P(10, y), the foci are F and F'. Then the condition is PF - PF' = 2a. The difference is taken from the farther focus, and and so the nearer focus. This on further substitutions and simplification nosotros have the equation of the hyperbola as \(\dfrac{ten^2}{a^ii} - \dfrac{y^2}{b^ii} = 1\).
What is a Rectangular Hyperbola?
The hyperbola having the major centrality and the pocket-size axis of equal length is chosen a rectangular hyperbola. Hence we accept 2a = 2b, or a = b. The equation of the rectangular hyperbola is x2 - y2 = a2.
What is the Standard Equation of Hyperbola?
There are two standard equations of the Hyperbola. These equations are given equally,
- \(\dfrac{ten^2}{a^ii} - \dfrac{y^2}{b^2} = 1\), for an hyperbola having the transverse centrality as the 10-axis and the cohabit axis is the y-axis.
- \(\dfrac{y^ii}{a^2} - \dfrac{x^ii}{b^2} = 1\), for an hyperbola having the transverse axis as the y-axis and its conjugate axis is the 10-axis.
What is the Eccentricity of Hyperbola?
The eccentricity of the hyperbola is greater than 1. (e > 1). The eccentricity is the ratio of the distance of the focus from the eye of the ellipse, and the distance of the vertex from the center of the ellipse. The distance of the focus is 'c' units, and the distance of the vertex is 'a' units, and hence the eccentricity is east = c/a. As well here we accept c2 = aii + bii.
What is the Foci of a Hyperbola?
The hyperbola has two foci on either side of its center, and on its transverse axis. The hyperbola \(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = one\) has two foci (c, 0), and (-c, 0).
What is the Conjugate Axis of a Hyperbola?
The axis line passing through the center of the hyperbola and perpendicular to its transverse axis is called the cohabit centrality of the hyperbola. The conjugate axis of the hyperbola having the equation \(\dfrac{ten^2}{a^2} - \dfrac{y^ii}{b^2} = 1\) is the y-axis.
What are Asymptotes of Hyperbola?
The asymptotes are the lines that are parallel to the hyperbola and are causeless to meet the hyperbola at infinity. The equation of asymptotes of the hyperbola are y = bx/a, and y = -bx/a. The equation of pair of asymptotes of the hyperbola is \(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^ii} = 0\).
What are the Vertices of a Hyperbola?
The vertices of a hyperbola are the points where the hyperbola cuts its transverse axis. The hyperbola has just two vertices, and the vertices of the hyperbola \(\dfrac{ten^ii}{a^2} - \dfrac{y^2}{b^2} = i\) is (a, 0), and (-a, 0) respectively.
How to Observe Transverse Axis of a Hyperbola?
The transverse axis of a hyperbola is a line passing through the centre and the two foci of the hyperbola. A hyperbola with an equation \(\dfrac{x^two}{a^two} - \dfrac{y^2}{b^2} = ane\) had the x-centrality as its transverse axis.
Standard Form Of A Hyperbola,
Source: https://www.cuemath.com/geometry/hyperbola/
Posted by: edwardsnots1968.blogspot.com


0 Response to "Standard Form Of A Hyperbola"
Post a Comment